اهمیت تحلیل کوواریانس در پژوهشهای روانشناختی
در مطالعات روانشناسی و علوم تربیتی، بررسی تأثیر مداخلاتی مانند آموزش تنظیم هیجانی بر متغیرهای پیامد (مانند سازگاری اجتماعی و مهارت حل مسئله) از اهمیت ویژهای برخوردار است. اما یک چالش اساسی وجود دارد: تفاوتهای اولیه بین شرکتکنندگان (مثلاً در پیشآزمون) ممکن است نتایج را تحت تأثیر قرار دهد. اینجاست که تحلیلهای کوواریانس (ANCOVA و MANCOVA) به کمک پژوهشگران میآیند.
چرا از این روشها استفاده میکنیم؟
-
کنترل اثر متغیرهای مداخلهگر (مانند نمرات پیشآزمون)
-
افزایش دقت در برآورد اثر مداخله
-
کاهش واریانس خطا
-
بهبود قدرت آماری پژوهش
فصل ۱: تحلیل کوواریانس تکمتغیره (ANCOVA)
۱.۱ ANCOVA چیست و چگونه کار میکند؟
تحلیل کوواریانس تکمتغیره (ANCOVA) ترکیبی از تحلیل واریانس (ANOVA) و رگرسیون خطی است که به ما امکان میدهد:
-
تأثیر یک یا چند متغیر مستقل (مانند گروه آزمایش/کنترل) را بر یک متغیر وابسته بسنجیم
-
همزمان اثر متغیرهای کمکی (مانند نمرات پیشآزمون) را کنترل کنیم
مثال کاربردی:
فرض کنید میخواهید تأثیر آموزش تنظیم هیجانی را بر سازگاری اجتماعی بررسی کنید. ANCOVA به شما کمک میکند اثر آموزش را پس از کنترل تفاوتهای اولیه در پیشآزمون بسنجید.
۱.۲ پیشفرضهای اساسی ANCOVA
| پیشفرض | روش بررسی | راهکارهای اصلاحی |
|---|---|---|
| نرمال بودن باقیماندهها | آزمون Shapiro-Wilk | تبدیل دادهها (مثلاً لگاریتمی) |
| همگنی واریانسها | آزمون Levene | استفاده از آزمونهای مقاوم |
| همگنی شیبهای رگرسیون | بررسی اثر تعاملی | حذف متغیر کمکی مشکلدار |
| خطی بودن رابطه | نمودار پراکندگی | افزودن جمله درجه دوم |
گام اول
گام دوم

گام سوم

گام چهارم
آزمون همگنی واریانس ها
گام پنجم
پیشفرض 2:
برابری واریانس (Levene)
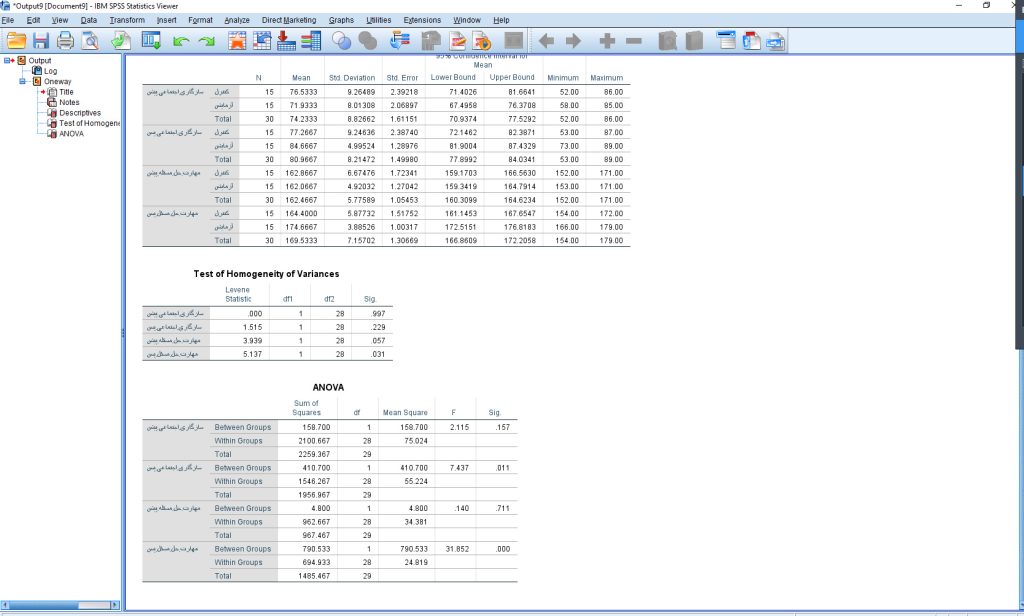
برابری واریانس (Levene)
۱.۳ مراحل اجرای ANCOVA در SPSS
۱. مسیر دسترسی:
Analyze > General Linear Model > Univariate

تحلیلهای تکمتغیره (ANCOVA):
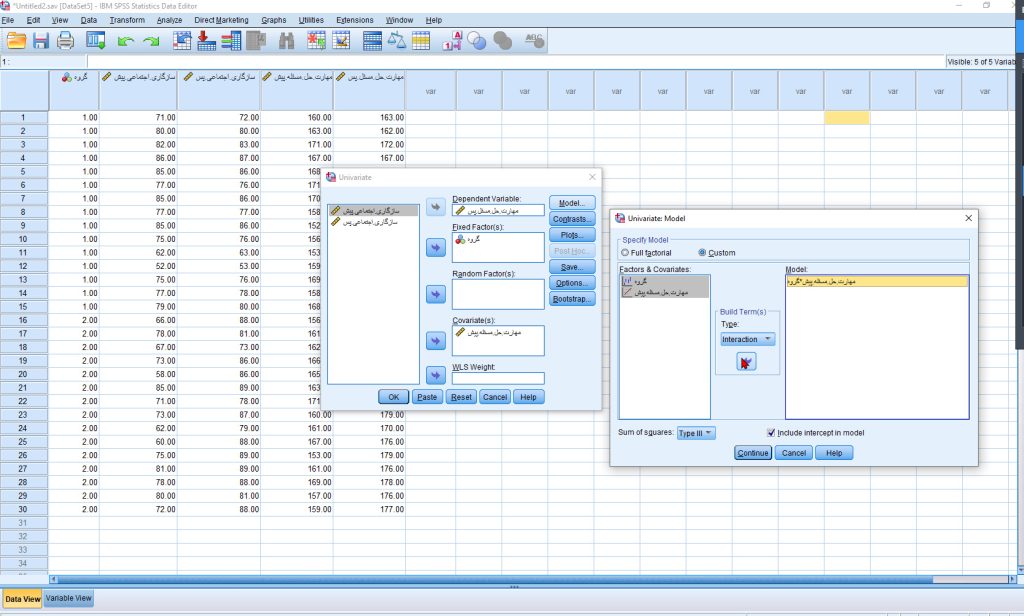
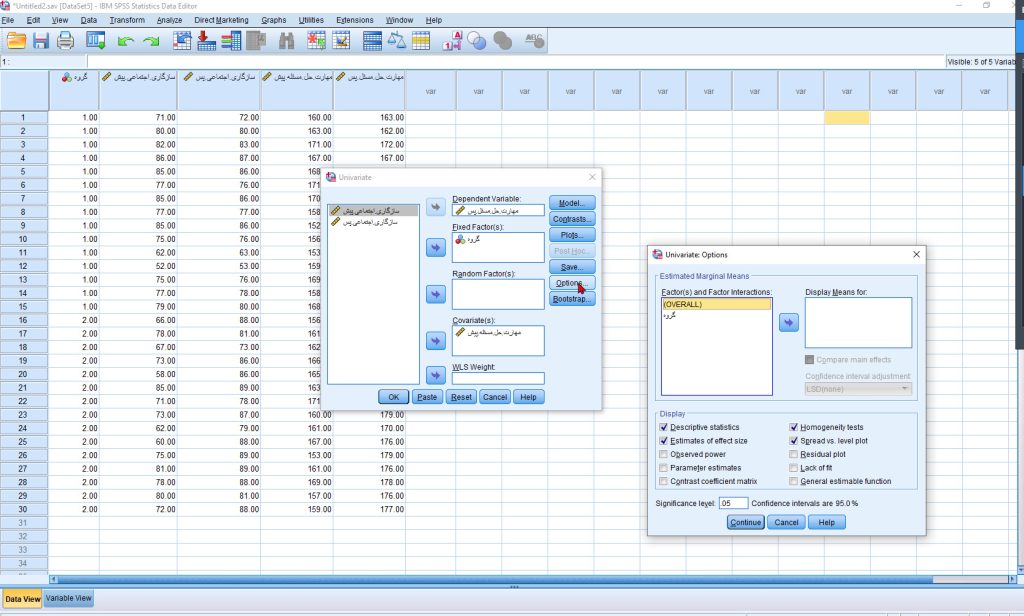
تحلیلهای تکمتغیره (ANCOVA): بررسی اثرات جداگانه روی هر متغیر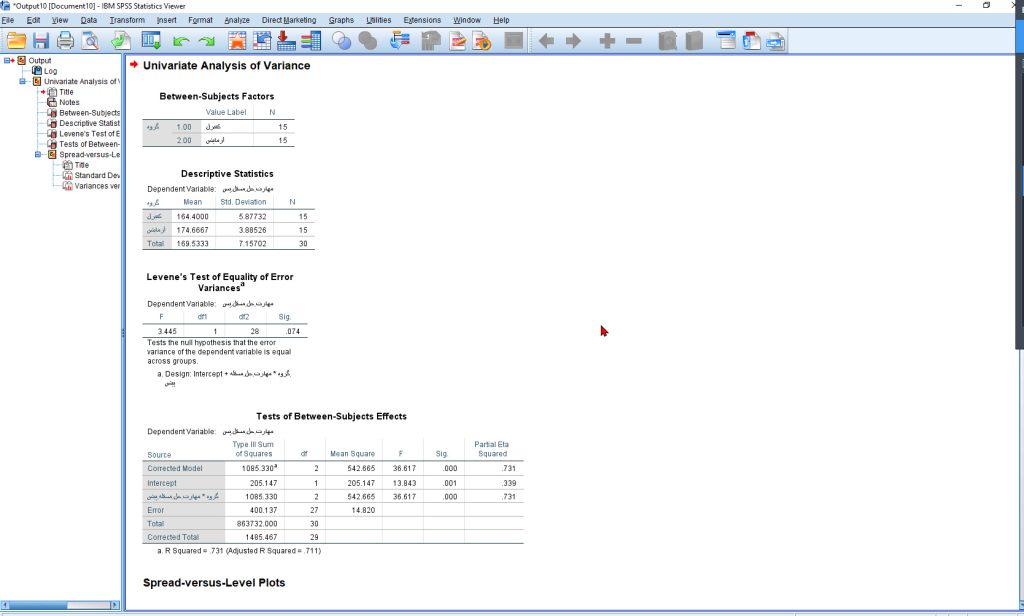
فصل ۲: تحلیل کوواریانس چندمتغیره (MANCOVA)
۲.۱ مزایای MANCOVA
-
امکان بررسی همزمان چندین متغیر وابسته
-
کنترل بهتر خطای نوع اول
-
بررسی روابط پیچیده بین متغیرها
-
افزایش قدرت آماری در صورت وجود همبستگی بین متغیرهای وابسته
۲.۲ پیشفرضهای کلیدی
۱. نرمال بودن چندمتغیره (آزمون Mardia)
۲. همگنی ماتریسهای کوواریانس (آزمون Box’s M)
۳. عدم همخطی چندگانه (بررسی ماتریس همبستگی)
۴. خطی بودن روابط (نمودارهای پراکندگی)

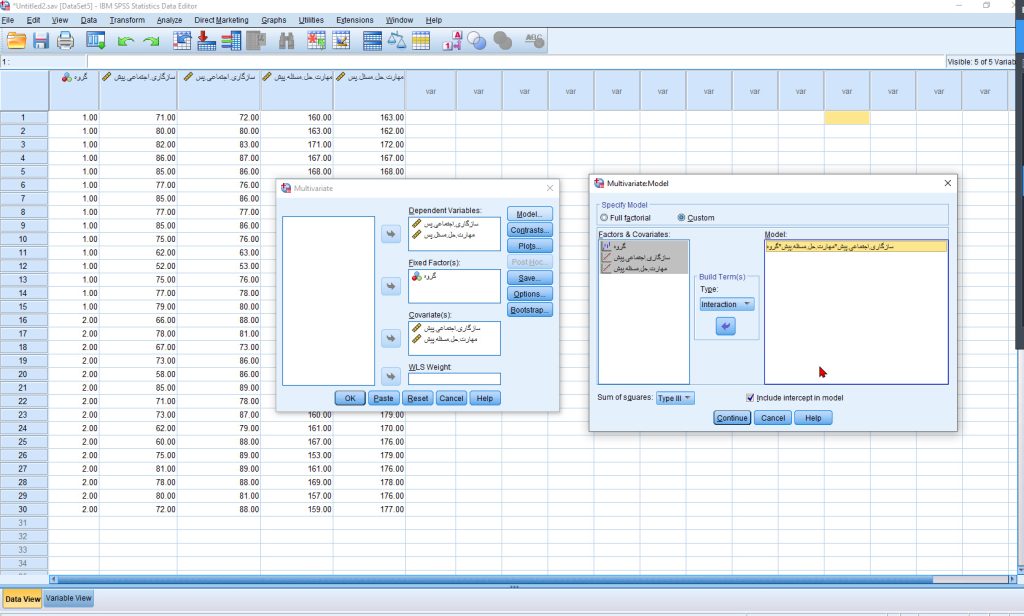

۲.۳ گامبهگام اجرای MANCOVA
۱. مسیر دسترسی:
Analyze > General Linear Model > Multivariate
۲. تعیین متغیرها:
-
متغیرهای وابسته: سازگاری اجتماعی و مهارت حل مسئله (پسآزمون)
-
متغیر مستقل: گروه
-
متغیرهای کمکی: نمرات پیشآزمون
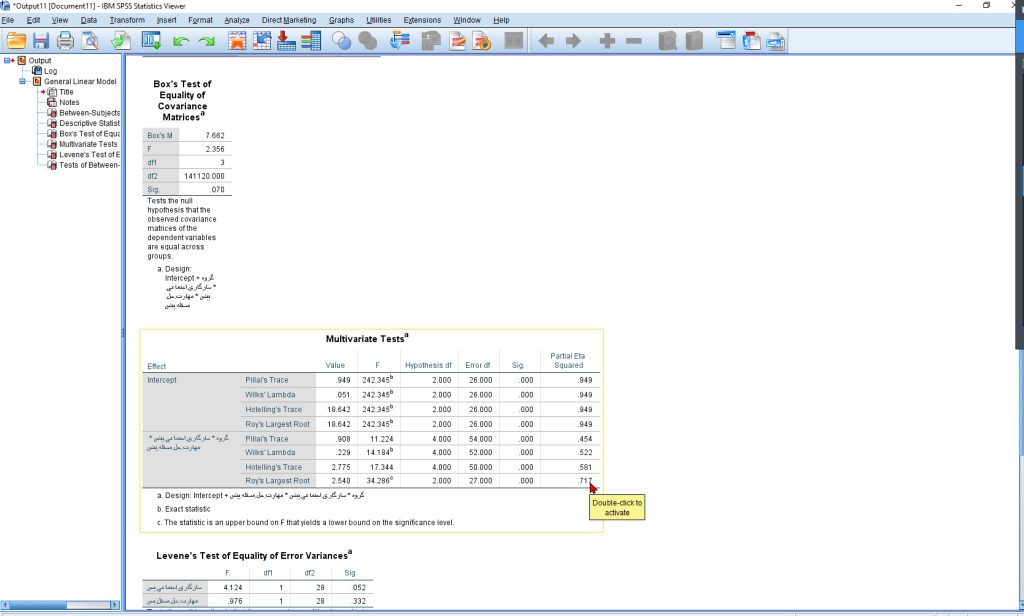
خروجی MANCOVA
آموزش کامل ویدیوئی