تحلیل آماری رابطه بین دو متغیر
۱. ضریب همبستگی (Correlation Coefficient) چیست؟
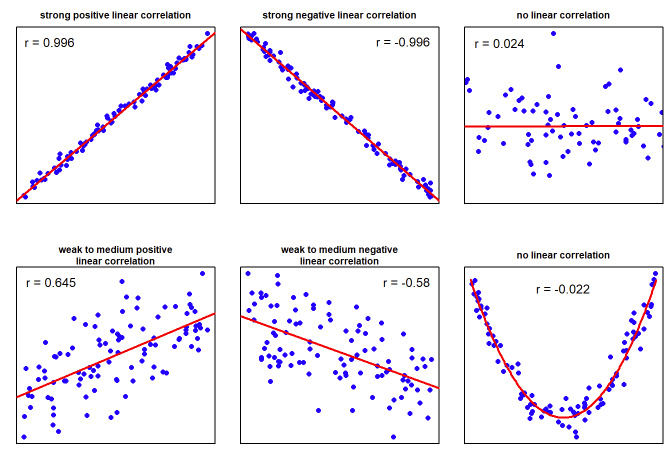
ضریب همبستگی یک شاخص آماری است که قدرت و جهت رابطهٔ خطی بین دو متغیر کمی (فاصلهای یا نسبی) را اندازهگیری میکند.
-
قدرت (Strength): نشان میدهد که دو متغیر چقدر به یکدیگر وابسته هستند. مقادیر نزدیک به +۱ یا -۱ نشاندهنده رابطه قوی، و مقادیر نزدیک به صفر نشاندهنده رابطه ضعیف یا عدم رابطه هستند.
-
جهت (Direction): نشان میدهد که با افزایش
انتخاب آماره صحیح، کاملاً به سطح سنجش (Measurement Scale) متغیرهای شما بستگی دارد. سطح سنجش به ویژگیهای دادهها اشاره دارد (اسمی، ترتیبی، فاصلهای، نسبی).
۱. ۱. متغیرهای با سطح سنجش اسمی (Nominal)
متغیرهای اسمی فاقد هرگونه ترتیب یا فاصله معنادار هستند (مانند: جنسیت، رنگ مو، شهرستان، نام برند).
-
آمارههای اصلی:
-
ضریب فی (φ – Phi Coefficient):
-
کاربرد: زمانی که هر دو متغیر، اسمی دوحالته (دوشقیه) باشند. (مثال: جنسیت (مرد/زن) و قبولی در آزمون (بله/خیر)).
-
محاسبه: بر اساس جدول توافقی ۲×۲ و خروجی آزمون خی-دو (χ²) محاسبه میشود. (
φ = √(χ² / n)). -
تفسیر: مقداری بین ۰ تا ۱ دارد. هرچه به ۱ نزدیکتر باشد، رابطه قویتر است.
-
-
ضریب وی کرامر (V – Cramer’s V):
-
کاربرد: زمانی که حداقل یکی از متغیرها اسمی با بیش از دو حالت باشد. (مثال: رابطه بین تحصیلات (دیپلم، لیسانس، فوقلیسانس) و نوع شغل (آزاد، دولتی، خصوصی)).
-
محاسبه: نیز بر پایه آزمون خی-دو است (
V = √(χ² / [n * (min(r-1, c-1))])). -
تفسیر: مقداری بین ۰ تا ۱ دارد. برای تفسیر قدرت رابطه از قوانین سرانگشتی استفاده میشود (مثلاً: ۰.۱=ضعیف، ۰.۳=متوسط، ۰.۵=قوی).
-
-
آزمون خی-دو استقلال (Chi-Square Test of Independence):
-
کاربرد: این آزمون، مبنای محاسبه ضرایب فی و وی کرامر است. این آزمون بررسی میکند که آیا بین دو متغیر اسمی رابطهای آماری معنادار وجود دارد یا خیر.
-
تفسیر: اگر سطح معنیداری (Sig. یا p-value) کمتر از ۰.۰۵ باشد (معمولاً)، فرض صفر (مبنی بر استقلال متغیرها) رد شده و نتیجه میگیریم بین متغیرها رابطه معنادار وجود دارد.
-
-
۱. ۲. متغیرهای با سطح سنجش ترتیبی (Ordinal)
متغیرهای ترتیبی دارای رتبه و ترتیب هستند، اما فاصله بین سطوح آنها برابر و مشخص نیست (مانند: سطح رضایت (کم، متوسط، زیاد)، مدرک تحصیلی، رتبه اجتماعی).
-
آماره اصلی:
-
ضریب همبستگی اسپیرمن (Spearman’s Rank Correlation Coefficient – ρ):
-
کاربرد: زمانی که هر دو متغیر ترتیبی باشند. همچنین زمانی که مفروضات همبستگی پیرسون (نرمال بودن، خطی بودن) برقرار نباشد، حتی برای دادههای فاصلهای/نسبی میتوان از اسپیرمن استفاده کرد.
-
محاسبه: بر اساس رتبههای دادهها محاسبه میشود، نه خود مقادیر خام.
-
تفسیر: مقداری بین ۱- تا ۱+ دارد.
-
جهت: علامت مثبت نشاندهنده رابطه همجهت (با افزایش رتبه یکی، رتبه دیگری نیز افزایش مییابد) و علامت منفی نشاندهنده رابطه معکوس است.
-
قدرت: مقادیر نزدیک به ۱+ یا ۱- رابطه قوی، و مقادیر نزدیک به صفر رابطه ضعیف را نشان میدهند.
-
-
-
۱. ۳. متغیرهای با سطح سنجش فاصلهای (Interval) و نسبی (Ratio)
این متغیرها علاوه بر ترتیب، دارای فاصلههای برابر و معنادار هستند. متغیر نسبی همچنین دارای نقطه صفر مطلق است (مانند: نمره آزمون، دما به سانتیگراد (فاصلهای)، سن، درآمد، قد (نسبی)).
-
آماره اصلی:
-
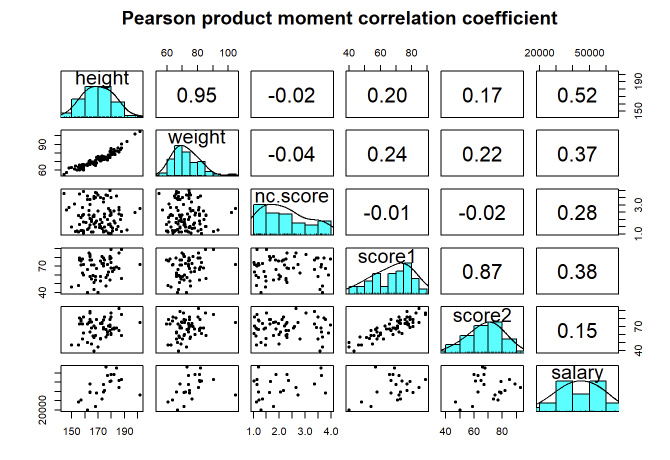
ضریب همبستگی گشتاوری پیرسون (Pearson Product-Moment Correlation Coefficient – r):
-
- کاربرد: زمانی که هر دو متغیر در سطح فاصلهای/نسبی باشند و رابطه بین آنها خطی باشد.
-
مفروضات کلیدی:
۱. رابطه بین متغیرها خطی است.
۲. دادهها به طور نرمال توزیع شدهاند (نرمالیته).
۳. واریانس دادهها در سطوح مختلف متغیرها یکنواخت است (هموسیاستیسیتی). -
محاسبه: بر اساس کوواریانس و انحراف معیار متغیرها محاسبه میشود.
-
تفسیر: مقداری بین ۱- تا ۱+ دارد.
-
جهت: مانند اسپیرمن، علامت مثبت و منفی جهت رابطه را نشان میدهد.
-
قدرت: قوانین رایج برای تفسیر قدرت رابطه پیرسون:
-
۰.۰ تا ±۰.۲: ضعیف یا هیچ
-
±۰.۲ تا ±۰.۴: ضعیف
-
±۰.۴ تا ±۰.۶: متوسط
-
±۰.۶ تا ±۰.۸: قوی
-
±۰.۸ تا ±۱.۰: بسیار قوی
-
-
-
۱. ۴. سایر حالات (Mixed Variables)
-
ضریب اتا (η – Eta Coefficient):
-
کاربرد: زمانی که یکی از متغیرها اسمی با دو یا چند گروه و متغیر دیگر فاصلهای/نسبی باشد. این ضریب برای تحلیل واریانس (ANOVA) استفاده میشود.
-
مثال: مقایسه میانگین قد (متغیر فاصلهای) در بین چندین استان مختلف (متغیر اسمی). ضریب اتا قدرت ارتباط بین استان و قد را نشان میدهد.
-
تفسیر: مقداری بین ۰ تا ۱ دارد و هرچه به ۱ نزدیکتر باشد، قدرت رابطه (تأثیر گروهبندی اسمی بر متغیر کمی) بیشتر است.
-
۲: خصوصیات و ملاحظات ضرایب همبستگی
۲. ۱. خصوصیات کلی ضرایب همبستگی
-
جهت (Direction): با علامت مثبت یا منفی نشان داده میشود که نشاندهنده همجهت یا غیرهمجهت بودن تغییرات دو متغیر است.
-
قدرت یا شدت (Strength): با مقدار مطلق ضریب سنجیده میشود. هرچه این مقدار به ۱ نزدیکتر باشد، رابطه قویتر است.
-
نوع رابطه (Form): میتواند خطی (مانند پیرسون) یا غیرخطی/رتبهای (مانند اسپیرمن) باشد.
۲. ۲. ملاحظات و هشدارهای بسیار مهم ضریب همبستگی
-
همبستگی علیت (Correlation does not imply Causation): این مهمترین اصل در تحلیل همبستگی است. حتی یک رابطه قوی و معنادار به این معنی نیست که یکی از متغیرها باعث تغییر در متغیر دیگر شده است. ممکن است متغیر سومی (متغیر مداخلهگر) باعث تغییر هر دو شده باشد، یا رابطه تصادفی باشد.
-
حساسیت به دادههای پرت (Sensitivity to Outliers): یک یا دو داده پرت میتواند به شدت بر مقدار ضریب همبستگی (به ویژه پیرسون) تأثیر بگذارد و آن را به طور کاذب افزایش یا کاهش دهد. همیشه دادهها را با نمودار پراکندگی (Scatter Plot) بررسی کنید.
-
محدوده دادهها (Restriction of Range): اگر تحلیل را فقط در یک محدوده خاص از دادهها انجام دهید، ممکن است رابطه واقعی را نبینید یا آن را ضعیفتر نشان دهید. (مثال: اگر رابطه هوش و پیشرفت تحصیلی را فقط بین دانشجویان دانشگاههای برتر بررسی کنید، ممکن است رابطه ضعیفی ببینید، چون دامنه هوش در این گروه محدود شده است).
-
خطی بودن رابطه (Linearity): ضریب پیرسون فقط رابطه خطی را اندازه میگیرد. ممکن است رابطه قوی اما غیرخطی (مثلاً منحنی) بین دو متغیر وجود داشته باشد که پیرسون قادر به تشخیص آن نیست.
-
تفسیر معناداری آماری در مقابل اهمیت عملی: یک همبستگی ممکن است از نظر آماری “معنادار” باشد (p-value < 0.05) اما مقدار آن بسیار کوچک باشد (مثلاً r=0.1). در چنین مواردی، اگرچه رابطه statistically significant است، اما از نظر عملی و در دنیای واقعی فاقد اهمیت و کاربرد است.
۳: تحلیل روابط علی بین متغیرها و ضریب همبستگی
همانطور که گفته شد، همبستگی به معنی علیت نیست. برای استنباط رابطه علی، باید شرایط سختگیرانهتری برقرار باشد:
۱. تقدم زمانی (Temporal Precedence): علت باید قبل از معلول رخ دهد.
۲. همایندی (Covariation): تغییر در علت باید با تغییر در معلول همراه باشد (همان چیزی که همبستگی نشان میدهد).
۳. حذف سایر توضیحات محتمل (Elimination of Alternative Explanations): باید ثابت شود که هیچ متغیر سومی (Confounding Variable) وجود ندارد که رابطه مشاهدهشده را توجیه کند.
روشهای پیشرفتهتری مانند تحلیل رگرسیون چندگانه، مدلسازی معادلات ساختاری (SEM)، و طراحیهای آزمایشی (Experimental Designs) برای بررسی روابط علی به کار میروند، چرا که میتوانند تا حدی اثر متغیرهای مداخلهگر را کنترل کنند.
۴: خدمات تخصصی ایران پروداکت: راهکاری مطمئن برای تحلیلهای آماری فوری و تضمینی
انجام تحلیلهای آماری با کیفیت، نیازمند دانش تخصصی، تجربه عملی و دقت فراوان است. خطا در هر مرحله، از انتخاب آزمون تا تفسیر نتایج، میتواند به نتیجهگیری کاملاً اشتباه منجر شود.
ایران پروداکت با گردآوری تیمی از متخصصان آمار و روش تحقیق، اینجا است تا بار سنگین تحلیلهای پیچیده را از دوش شما بردارد.
چرا خدمات تحلیل آماری ایران پروداکت را انتخاب کنید؟
-
تضمین کیفیت و دقت: تمامی خروجیها توسط دو متخصص مجزا بررسی و تضمین میشوند.
-
سرعت و انجام فوری: پروژههای شما با اولویت زمانی خودتان و در کوتاهترین زمان ممکن انجام میشود.
-
پشتیبانی و اصلاح تا مرحله نهایی: ما تا دریافت نهاییترین تایید از سمت شما (از سوی استاد راهنما، مجله، یا داوران) در کنارتان هستیم.
-
تفسیر حرفهای و قابل درک: خروجی نهایی ما تنها یک خروجی نرمافزاری نیست، بلکه شامل گزارشی کامل و کاربرپسند به زبان فارسی است که یافتهها به وضوح تفسیر شدهاند.
-
مشاوره رایگان در انتخاب روش: حتی اگر مطمئن نیستید از کجا شروع کنید، با ما تماس بگیرید تا بهترین مسیر را به شما نشان دهیم.
برای سفارش تحلیل آماری فوری و تضمینی خود، به وبسایت ایران پروداکت مراجعه کنید یا از طریق راههای ارتباطی با ما در تماس باشید.
۵: رویکرد آموزشمحور و کوچینگ دانشجویی: سرمایهگذاری برای آینده
ما در ایران پروداکت باور داریم که ارائه خدمات محض، اگرچه مشکل فعلی را حل میکند، اما دانشجو یا پژوهشگر را برای چالشهای آینده آماده نمیسازد. بنابراین، ما یک پکیج ویژه آموزشمحور و کوچینگ (Coaching) ارائه میدهیم.
این پکیج برای کسانی طراحی شده است که میخواهند:
-
به صورت پایهای و اصولی علم آمار و روش تحقیق را فرابگیرند.
-
بتوانند در آینده به طور مستقل و با اطمینان تحلیلهای خود را انجام دهند.
-
از مسیر پایاننامه یا رساله خود نه به عنوان یک دردسر، بلکه به عنوان فرصتی برای یادگیری و رشد استفاده کنند.
مزایای کوچینگ دانشجویی ایران پروداکت:
-
جلسات آموزشی خصوصی و آنلاین با متخصصان باتجربه.
-
یادگیری گامبهگام نرمافزارهای آماری (SPSS, AMOS, PLS, etc.) همراه با پروژه عملی.
-
هدایت و منتورینگ در تمام مراحل پژوهش از تعریف مسئله تا تدوین نهایی گزارش.
-
تمرکز بر “چرا”ها: به جای حفظ کردن طوطیوار، به شما میآموزیم که چرا هر آزمونی را انتخاب و چگونه آن را تفسیر میکنیم.
-
افزایش اعتمادبهنفس علمی برای دفاع از پایاننامه و ارائه مقالات.
با انتخاب این مسیر، شما تنها یک تحلیلگر آماری استخدام نکردهاید؛ یک مربی و همراه علمی برای کل مسیر پژوهش خود دارید.
۶: سوالات متداول (FAQ)
۱. تفاوت اصلی بین همبستگی پیرسون و اسپیرمن چیست؟
-
پیرسون: رابطه خطی بین دو متغیر فاصلهای/نسبی با توزیع نرمال را اندازه میگیرد.
-
اسپیرمن: رابطه یکنواخت (چه خطی و چه غیرخطی) بین دو متغیر ترتیبی را بر اساس رتبه دادهها اندازه میگیرد. اگر مفروضات پیرسون برقرار نباشد، از اسپیرمن برای دادههای فاصلهای/نسبی نیز استفاده میشود.
۲. اگر سطح معنیداری (p-value) کوچک باشد اما ضریب همبستگی نیز کوچک باشد، چه تفسیری دارد؟
این حالت معمولاً در نمونههای بسیار بزرگ (مثلاً بیش از ۱۰۰۰ نفر) رخ میدهد. در این حجم نمونه، حتی روابط بسیار ضعیف نیز از نظر آماری “معنادار” تشخیص داده میشوند. در اینجا باید بر مقدار ضریب همبستگی و اهمیت عملی آن تأکید کرد. چنین رابطهای اگرچه معنادار است، اما از نظر کاربردی قوی محسوب نمیشود.
۳. چگونه میتوانم نرمال بودن دادهها برای استفاده از پیرسون را بررسی کنم؟
از آزمونهای نرمالیته مانند کلموگروف-اسمیرنوف (K-S) یا شاپیرو-ویلک (Shapiro-Wilk) و همچنین نمودارهایی مانند Q-Q Plot یا هیستوگرام استفاده کنید.
۴. اگر یکی از متغیرهایم اسمی (با سه گروه) و دیگری فاصلهای باشد، از چه آزمونی استفاده کنم؟
از تحلیل واریانس یکطرفه (One-Way ANOVA) استفاده کنید. خروجی این آزمون شامل ضریب اتا (η) است که قدرت ارتباط را نشان میدهد.
۵. ضریب همبستگی من ۰.۹- شده است. آیا این رابطه ضعیف است؟
خیر. علامت منفی فقط جهت رابطه را نشان میدهد. مقدار مطلق ۰.۹ نشاندهنده یک رابطه بسیار قوی اما معکوس است. یعنی با افزایش یکی، دیگری به طور سیستماتیک کاهش مییابد.
۶. حداقل حجم نمونه برای تحلیل همبستگی چقدر است؟
یک قاعده سرانگشتی رایج، حداقل ۳۰ مشاهده است. اما این عدد بستگی به قدرت اثر مورد انتظار و تعداد متغیرها دارد. برای اطمینان، بهتر است از نرمافزارها یا جداول مخصوص محاسبه حجم نمونه استفاده کنید.
۷. آیا میتوانم همبستگی را برای بیش از دو متغیر انجام دهم؟
بله. از ماتریس همبستگی استفاده میشود که همبستگی بین هر جفت از متغیرها را در یک جدول نمایش میدهد.
۸. اگر دادههای پرت داشته باشم چه کار کنم؟
اولاً باید با نمودار پراکندگی آنها را شناسایی کنید. سپس باید بررسی کنید که آیا این دادهها ناشی از خطای ثبت هستند یا واقعی. اگر واقعی هستند، میتوانید:
-
از ضریب اسپیرمن استفاده کنید که نسبت به دادههای پرت مقاومتر است.
-
در شرایط خاص و با توجیه قوی، آنها را از تحلیل حذف کنید.
-
از روشهای رگرسیون مقاوم (Robust Regression) استفاده کنید.
۹. تفاوت ضریب فی و وی کرامر در چیست؟
ضریب فی مخصوص جداول ۲×۲ است. در حالی که وی کرامر تعمیمی از ضریب فی برای جداول بزرگتر (مثلاً ۳×۳، ۴×۵ و …) است و مقدار آن برای جدول ۲×۲ با فی برابر خواهد بود.
۱۰. چگونه خروجی همبستگی اسپیرمن را در SPSS تفسیر کنم؟
به دو بخش نگاه کنید:
-
ضریب همبستگی (Correlation Coefficient): قدرت و جهت رابطه.
-
سطح معنیداری (Sig. 2-tailed): اگر این مقدار کمتر از ۰.۰۵ باشد، رابطه از نظر آماری معنادار است.
۱۱. آیا میتوان از همبستگی برای پیشبینی استفاده کرد؟
همبستگی به تنهایی برای پیشبینی کافی نیست. برای پیشبینی مقدار یک متغیر بر اساس متغیر دیگر، باید از تحلیل رگرسیون استفاده کنید. همبستگی مبنای رگرسیون است.
۱۲. رابطه بین “ضریب تعیین” و ضریب همبستگی چیست؟
ضریب تعیین (R²) مجذور ضریب همبستگی پیرسون (r) است. این ضریب نشان میدهد که چند درصد از واریانس (تغییرات) یک متغیر، توسط واریانس متغیر دیگر توضیح داده میشود. مثلاً اگر r=0.6 باشد، R²=0.36 خواهد بود، یعنی ۳۶٪ از تغییرات یک متغیر توسط متغیر دیگر تبیین میشود.
۱۳. اگر دادههایم ترتیبی باشند اما از فاصلههای مساوی برخوردار باشند (مثل مقیاس لیکرت)، از پیرسون استفاده کنم یا اسپیرمن؟
این یک منطقه خاکستری است. بسیاری از پژوهشگران به دلیل ماهیت “فاصلهای فرض شده” دادههای لیکرت، از پیرسون استفاده میکنند. اما محافظهکارانهتر این است که از اسپیرمن استفاده شود، زیرا دادههای لیکرت به طور ذاتی ترتیبی هستند. بهترین کار این است که هر دو را بررسی کنید. اگر نتایج هر دو مشابه بود (که معمولاً هست)، با اطمینان بیشتری گزارش میکنید.
۱۴. خدمات ایران پروداکت برای چه مقاطعی مناسب است؟
تمامی مقاطع تحصیلی از کارشناسی (برای پروژههای درسی و پایانی) گرفته تا کارشناسی ارشد (پایاننامه) و دکتری (رساله و مقالات علمی-پژوهشی) و حتی پژوهشگران حرفهای در سازمانها میتوانند از خدمات ما بهرهمند شوند.
۱۵. چگونه میتوانم در پکیج کوچینگ دانشجویی ثبتنام کنم؟
کافی است از طریق وبسایت ایران پروداکت با ما تماس بگیرید. یک جلسه مشاوره رایگان برای شنیدن نیازهای شما و ارائه طرحی متناسب با اهداف و زمانبندیتان برگزار خواهیم کرد.
کلام پایانی: تحلیل آماری، زبان گویای دادههای شماست. این زبان را یا با کمک مربیان مجرب ما به خوبی فراخواهید گرفت، یا کار ترجمه آن را به ما میسپارید تا با خیال راحت بر روی مفاهیم و ایدههای بزرگتر پژوهش خود تمرکز کنید. انتخاب با شماست.
موفق و پیروز باشید.
تیم پشتیبانی ایران پروداکت